Altijd een moeizaam moment in de spelshow 2 voor 12… Je ziet de ogen van de kandidaten afdwalen naar de boekenkast in de studio. Gaan ze vertrouwen op parate kennis of duiken ze toch nog in een van die dikke naslagwerken?
Deze vraag (of je beter een antwoord kan opzoeken of kan raden) is prima te beantwoorden aan de hand van de economische nutstheorie. In dit artikel leg ik uit hoe dat in zijn werk gaat.
Om te beginnen moeten we rekening houden met de manier waarop punten worden toegekend in het spel:
- Beginpunten: Teams beginnen met 500 punten. Niet zo relevant, maar om een compleet beeld te schetsen.
- ‘Strafpunten’ voor opzoeken (-1 punt per 2 seconden opzoeken)
- Bonussen voor het aantal fouten (0 fout: +100 punten, 1 fout: +75 punten, 2 fouten: +50 punten, 3 fouten: +25 punten)
- Bonus voor goede antwoorden uit het hoofd (+10 per antwoord)
Verwachtingswaarde berekenen
Je kunt de verwachtingswaarde per individuele vraag als volgt berekenen. Eerst formuleren we de variabelen:
- P is de kans dat je het antwoord uit het hoofd goed hebt.
- C is het aantal punten dat de score toeneemt met een goed antwoord.
NB: Als je drie of minder fout hebt in totaal, dan geldt altijd C = 25, omdat je voor elke elke fout die je minder maakt 25 extra bonuspunten krijgt. Een belangrijke aanname bij deze berekening is dan ook dat je sowieso maximaal vier fouten maakt. - R is het aantal strafpunten voor het opzoeken van een antwoord (het aantal opzoekseconden gedeeld door twee).
De verwachtingswaarde van een antwoord uit het hoofd geven (inclusief 10 bonuspunten) ziet er zo uit:
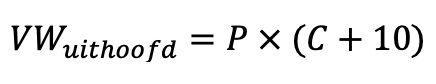
NB: Bij de verwachtingswaarde voor een opgezocht antwoord ga ik er gemakshalve van uit van een kans van 100% dat het antwoord goed is, oftewel P = 1. In het echt is dat ook wel eens anders. De verwachtingswaarde ziet er daarom zo uit:
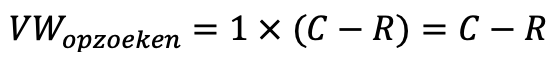
Om te bepalen of je beter kunt opzoeken of het antwoord uit je hoofd geven, moet je beide verwachte waarden aan elkaar gelijk stellen:
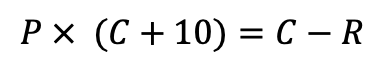
We willen de waarschijnlijkheid P te weten komen. Daar kun je als volgt achter komen:
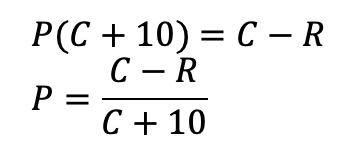
Die laatste vergelijking biedt het gereedschap om P te weten te komen, en een onderbouwde beslissing te nemen over of je een antwoord uit je hoofd kunt geven, of dat je beter kunt opzoeken. Het enige dat je zelf moet inschatten is hoe lang je erover zou doen om het goede antwoord op te zoeken (met als gevolg het aantal ‘strafpunten’ R).
Voorbeelden
Stel: je hebt naar verwachting twintig seconden nodig om het juiste antwoord te vinden. Hoe zeker moet je zijn van een goed antwoord uit het hoofd, om niet te gaan zoeken?
We weten dat twintig seconden zoektijd neerkomt op R = 10, oftewel tien ‘strafpunten’.1
Dat leidt tot het volgende beeld:
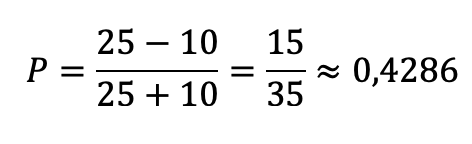
Hoe interpreteren we deze uitkomst? Als de kans ongeveer 43% of meer is dat het antwoord uit het hoofd juist is, dan is de optimale keuze om het antwoord uit het hoofd te geven, in plaats van het goede antwoord binnen twintig seconden op te zoeken.
De drempel om het antwoord tóch uit het hoofd te geven wordt hoger als het opzoeken minder tijd kost. Stel dat je een Wiki-vraag bijvoorbeeld in twee seconden kunt opzoeken (leidend tot één strafpunt, of P = 1), dan moet de kans dat het uit het hoofd goed is ongeveer 69% of hoger zijn.
Onderstaande figuur (die uitgaat van C = 25) toont tot slot hoe P zich ontwikkelt naarmate de zoektijd (en dus het aantal strafpunten R) toeneemt. Het laat aardig zien dat als je volgens de economische nutstheorie 50 seconden (R = 25) of langer aan het zoeken bent, je eigenlijk beter een fout antwoord uit het hoofd kunt geven (formeel: een antwoord met een kans van 0% dat het goed is).2
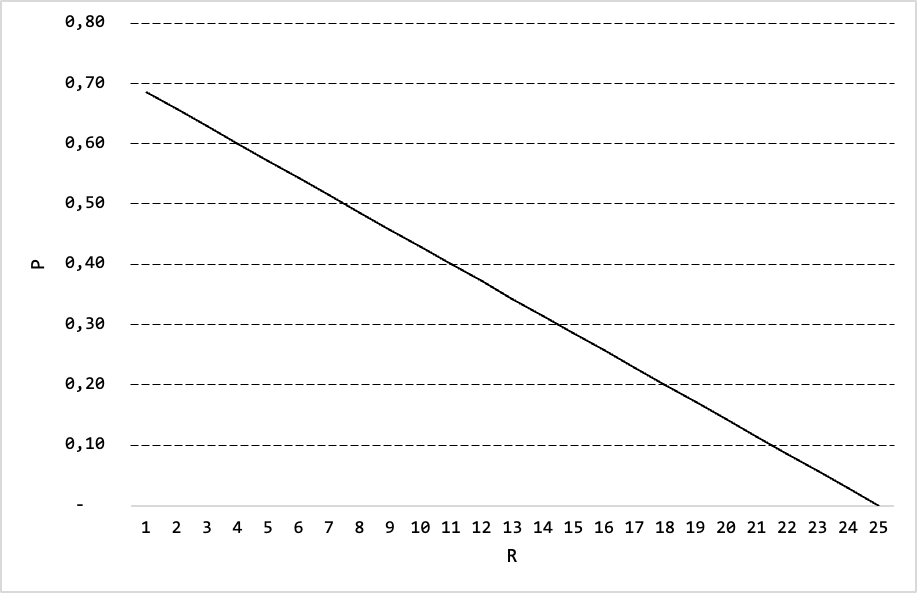
Besluit
Ga met deze bagage maar eens kijken hoe de kandidaten bij 2 voor 12 het ervan af brengen. Zijn de keuzes die ze maken optimaal? Of blijven ze hopeloos lang (nu weet je: langer dan 50 seconden) zoeken naar een antwoord, waardoor fout uit het hoofd antwoorden eigenlijk optimaler was geweest voor de eindstand? Of andersom: compenseert hun zoeksnelheid juist uitstekend voor het verlies van de bonuspunten?
Leuke vragen, waar jij nu als economisch mens het antwoord op hebt.
Resteert alleen nog de vraag hoe je in het heetst van de strijd de kans inschat dat jouw antwoord uit het hoofd goed is. In de praktijk is dat immers niet hetzelfde als hoe overtuigd jijzelf van je goede antwoord bent. Als je dit leest en je hebt een achtergrond in de gedragseconomie, dan zou ik zeggen: leef je uit op deze vraag.
Behoefte aan nog meer blogs over 2 voor 12? Lees ook:
- Oefen de Taartpuzzel uit 2 Voor 12 op bijna 15.000 woorden met deze eenvoudige spreadsheet
- Oefen het twaalfletterwoord uit 2 Voor 12 op bijna 20.000 woorden met deze eenvoudige spreadsheet
- Oefen de Paardensprong uit 2 Voor 12 op bijna 15.000 woorden met deze eenvoudige spreadsheet
Ik vraag geen geld voor deze blog, maar als je dit leuk of nuttig vond en me financieel wil steunen, dan mag dat natuurlijk! Dat doe je via ↗️️Buy Me A Coffee. Veel dank!
- Een verwarrend voorbeeld, realiseer ik me nu, want aan de andere kant van de vergelijking krijg je 10 tien bonuspunten voor uit het hoofd. Nou ja, een gewaarschuwd mens, enzovoorts. ↩︎
- Tenzij het natuurlijk een cruciale letter is om het woord te kunnen raden, maar dat onderwerp vormt geen onderdeel van dit model. ↩︎